
He needs to know if they're equally difficult so he asks his students to complete all 3 exams in random order. You should now be able to run a one sample t test in SPSS, and to interpret the result that you get.SPSS Paired Samples T-Test Tutorial By Ruben Geert van den Berg under Statistics A-Z & T-TestsĪ paired samples t-test examines if 2 variablesĪre likely to have equal population means.Ī teacher developed 3 exams for the same course. Put simply, it seems that our subjects fall to sleep in statistics lessons more quickly than is true of the population as a whole. This counts as evidence that the difference between our sample group and the population as a whole is real. More technically, what the result shows is that on the assumption that the null hypothesis is true, a difference as big as we’ve got between our sample mean and the population mean is extremely unlikely to have arisen purely by chance. 05, so we’re going to reject the null hypothesis which asserts there is no difference between our sample mean and the population mean. This is going to be a significant result for any realistic alpha level.Ī standard alpha level is. The t value is -4.691 (see the One-Sample Test table, above), which gives us a p-value (or 2-tailed significance value) of. This output is relatively easy to interpret. The result of the one sample t test will appear in the SPSS output viewer. If you’ve got this far, you’re ready to run the test. Once it’s set up, it should look like this.
For the variable, you can just drag and drop, or use the arrow in the middle of the dialog box.

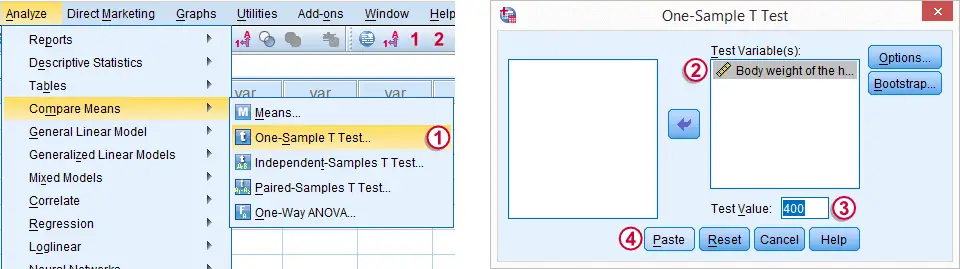
You’ve got to get the variable you want to test – in our case, the Duration variable – into the right hand Test Variable(s) box, and input the population mean into the Test Value box. This will bring up the One-Sample T Test dialog box. To begin the one sample t test, click on Analyze -> Compare Means -> One-Sample T Test. If we knew the population standard deviation, we could do a z test to answer this question, but we don’t, which means a one sample t test is the appropriate test. The question is whether the difference between these two means is large enough for us to conclude there is a real difference between our sample group and the wider population in terms of the amount of time it takes to fall asleep. This compares to the average time in our sample of 7.35 minutes. Imagine we already know that in the population as a whole the average amount of time it takes for somebody to fall asleep is 8.45 minutes. Our data is from a hypothetical study that examines how long it takes people to fall asleep during a statistics lesson.įor the purpose of this tutorial, we’re only interested in the Duration variable, which is the number of minutes that elapses from the start of the lesson before a subject falls asleep. Our working assumption, as per usual, is that you’ve opened SPSS, and that you’re looking at the Data View within which you’ve got some data. Your result will appear in the SPSS output viewer.Specify your population mean in the Test Value box.Drag and drop the variable you want to test against the population mean into the Test Variable(s) box.Analyze -> Compare Means -> One-Sample T Test.


 0 kommentar(er)
0 kommentar(er)
